The Superpressure Balloons Vol. 2

The first blog on superpressure balloons ended when I finished the first two envelopes in mid April. Right after that, I followed the same method and made one more smaller balloon and one quite large envelope 2.66m in diameter. Both, however, failed at some point during stretching. And that was it until the end of July. At that point I had finalized all five trackers, and with the middle of August in mind as the time to start launching, I set off to finish the remaining balloons.

No.	Type	Size	Marking	Date	Note
1	Sphere	1.33	first	April	TT7F1
2	Sphere	1.84	first	April	TT7F3
3	Sphere	1.33	second	April	hole in stretched area
4	Sphere	2.66	first	April	meridional weld opening (repeatedly)
5	Sphere	1.33	n1	July	hole in stretched area
6	Sphere	1.33	n2	July	hole in stretched area
7	Sphere	1.33	n3	July	TT7F2
8	Sphere	1.84	n1	August	hole at the edge of repaired meridional weld
9	Sphere	1.84	n2	August	TT7F4
10	Sphere	1.84	n3	August	hole at the edge of repaired filling tube weld
11	Sphere	2.66	n1	August	hole in meridional weld opening
12	Sphere	1.84	n4	August	unintentionally sealed filling tube
13	Sphere	1.84	n5	August	circumferential weld opening (repeatedly)
14	Sphere	1.84	n6	August	meridional weld opening (new heat element wire)
15	Sphere	1.84	n7	August	hole in meridional weld opening
16	Sphere	1.33	n4	August	hole in stretched area
17	Tube	3.33	n1	September	TT7F5
18	Tube	2.33	n1	September	TT7F6W

The table above, summarizing all the balloons I had to make, suggests it wasn't as straightforward as I would like. I encountered a number of issues a portion of which originated in the need to redo some of the welds after they had opened during initial stretching. Another portion due to weak spots in the material itself. Usually, the failures of the smaller envelopes were the second type showing itself as small breaches in some layer(s) of the film that with further stretching eventually burst. I am not sure about the origin of these seemingly randomly appearing spots, but they do limit the extent to which the stretching can proceed. The larger envelopes, made of more individual pieces, mostly suffered from weld openings. Particularly problematic was the meridional weld which is located in the area of the highest stress. In S1.84_n3 and S1.84_n4, I tried to get round this issue with a different construction method which saw the meridional weld replaced by two shorter welds further from the main stress area. However, the result was the same. At one point, I started to notice an inability of the heat sealer to produce reliable welds. Over the course of several envelopes, I attempted to repeatedly repair the connections between the heat element wire and the rest of the circuit, and periodically check the weld quality with test stripes that I could stretch and examine. None of this, though, brought success. I also contemplated following the example of others and make my own heat sealer for a while, but in the end being pursued by the intended launch dates, I decided to stick to the current device. I did, however, buy a new heat element wire which significantly improved the weld quality. I still failed with a few more spherical envelopes, but eventually after trying a different shape (tube balloon), I finally worked my way to promising results again.

For illustration, these are images of good circumferential welds in early stages of stretching (top two) and then later stages (bottom two) where all the deeper bends have been stretched out.

These images show examples of plastic deformation during and after hours of stretching. As can be seen, the deformation isn't uniform, but rather localized, due to the uneven shape of the balloon, to areas of the highest stress. The envelope is still sealed and these 'stretching marks' are considered ok.

These are examples of the small breaches in film that tend to appear as stretching progresses. I haven't noticed any regularity in spacing between individual breaches that would suggest a single impact on the whole roll of film. Among other possible causes is my handling of the film. It sometimes gets to crumple at one spot before I straighten it. Another potential cause could be the manufacturing process of the film itself. I don't know whether others who made their own balloons encountered this issue with the films they used or not.

The later stages of the local breaches in film can be seen in the images above. Upon further stretching the material eventually ruptures. I haven't found a way to repair this sort of a failure. The stretched film around the hole is no longer reliably weldable.

The circumferential weld on a spherical (Mylar balloon shape) balloon is located in area of least stress. Hence, it doesn't suffer from openings as much as the meridional weld. Although an inconsistent heat sealer (ageing heat element wire for example) can lead to poorer circumferential welds as in S1.84_n5. This issue seems to be repairable to an extent. Mainly, if the material hasn't undergone too much plastic deformation. The picture on the right shows another weld gradually opening on the differently constructed S1.84_n3.

The most frequent issue on the larger envelopes made of four individual pieces (S1.84 and S2.66) was the meridional weld not sustaining the stress and eventually opening. In retrospect, I would accredit this issue in a number of the cases to the heat sealer not producing reliable welds consistently at that time. Also the potential of successfully repairing the weld again is low, because the material in this area deforms right from the beginning making it not respond properly to the heat sealing anymore.

These images come from S2.66_n1 and S1.84_n7 and depict a failure due to a hole developing in the meridional weld opening. In the first case, it was after I repaired a meridional weld opening by welding the deformed material. The second case shows another issue I had with the heat sealer. When doing straight welds that are longer then the heat sealer itself, it tends to deform the film right at the end and a little beyond. I suspect that in this case it burnt through the film resulting in a small hole too close to the edge.

Flight	Type	kg	m3	Γ	m3
TT7F1	S1.33	0.136	0.358	1.94	0.695
TT7F2	S1.33	0.136	0.358	1.93	0.691
TT7F3	S1.84	0.260	0.949	1.83	1.737
TT7F4	S1.84	0.260	0.949	1.74	1.651
TT7F5	T3.33	0.395	1.484	1.35	2.003
TT7F6	T2.33	0.265	0.921	1.51	1.391

I should also reflect on the volume and mass estimates of individual envelopes I have made. The table above shows the estimated mass and volume of the individual envelopes used on specific flights followed by the estimated Gamma and final volume estimate after stretching. Starting with the spherical (Mylar balloon shaped) balloons, throughout manufacture and stretching I used the equation provided by Wikipedia: $$V = \frac{2}{3} \pi a r^2$$ to calculate the volume estimate. Where $a$ is one fourth of the meridional circumference (radius of deflated envelope) and $r = 0.763 a$ (radius of inflated envelope). Throughout stretching, I periodically measured the meridional circumference and recalculated the volume. To calculate the mass estimate: $$m = 2\frac{\pi d^2}{4} \cdot t \cdot \rho$$ where the first part of the equation corresponds to the area of the two flat sheets of film which is then multiplied by the material thickness $t$ and density $\rho$. Having that many failed envelopes, I eventually used them to measure the mass directly, and found that the real mass differed by a factor of 1.079-1.089 to the calculated estimates. Following with the tube balloon estimates, I used: $$V= \frac{2}{3} \pi a r_{1}^2 + \pi r_{2}^2 l$$ to calculate the volume. It is basically an S1.33 Mylar shape balloon split by a cylinder of length $l$. The radius $r_{1}$ relates to the Mylar shape balloon while $r_{2}$ is the cylinder's radius of circumference $4a$ thus $r_{2} = 4a / \pi / 2$. During the stretching process, I measured the circumference in two different places, because the balloon expanded unevenly. To reflect that, I calculated the average circumference $(c_{mid} + c_{edge}) / 2$ and used it instead. For the mass estimate: $$m =(2\frac{\pi d^2}{4} + 2 d l) \cdot t \cdot \rho$$ where $2dl$ corresponds to the area of the cylindrical section. In case of the tube envelopes, I didn't have any failed ones and didn't want to fold the flight ready envelopes to fit it on a scale, so I simply adjusted the estimates by the previously derived factor of 1.08, and used these values in the consequent lift calculations.

These are the stretching profiles of all six envelopes that were launched with the running estimates performed as described. Generally, I would schedule a pressurizing scheme that would slow down the rate higher the pressure was all the way towards a specific pressure level inside the balloon. I would in intervals measure the increase in circumference rising the pressure level if the expansion stopped. All along I'd be examining the envelope, looking out for the local breaches in film mentioned earlier. My initial aim was to stretch and pressurize the balloon to a level corresponding to the expected superpressure (including the effect of maximum expected supertemperature) at the expected float altitude. However, this turned out to be tricky to achieve, and as the first launch later revealed, my volume estimates were way off. In the end, breaches in film layers and early stages of weld openings became the decisive factors in when to end the stretching.

Flight	Type	kg (b)	kg (p)	kg (fl)	kg (h)	m	Pa	°C	m3	%
TT7F1	S1.33	0.148	0.0134	0.0112	0.0129	11242	23285	-51.6	0.476	68.5
TT7F2	S1.33	0.148	0.0197	0.0108	0.0134	10524	25900	-46.4	0.455	65.8
TT7F3	S1.84	0.283	0.0319	0.0156	0.0247	13403	16573	-62.7	1.237	71.2
TT7F4	S1.84	0.283	0.0315	0.0183	0.0249	11864	20341	-56.4	1.038	62.8
TT7F5	T3.33	0.427	0.0354	0.0110	0.0354	12226	18782	-57.4	1.641	81.9
TT7F6	T2.33	0.287	0.0210	0.0073	0.0236	12153	20342	-61.8	0.988	71.1

This table sums up the actual masses of the envelopes (b) and payloads (p), the actual amounts of free lift (fl) to which I managed to fill the balloons, the corresponding amount of hydrogen (h), the actual float altitudes, and back calculated values of the envelope volumes. Following the volume figure is a column comparing the back calculated value to the original estimate. For the calculation itself, I interpolated pressure and temperature values corresponding to the float altitude from the closest atmospheric sounding data. $$V = \frac{m_b + m_p + m_g}{p_{air} / R_{air} / T_{air}}$$ The equation is a specific form of the ideal gas law. Since at float altitude, the density of the system is in equilibrium with the density of the surrounding air, the volume of the system (majority of which is the balloon) equals to the mass of the whole system (balloon, payload and gas) divided by the air density. $R_{air}=286.9 \, J/kgK$ is the specific gas constant of air and $T_{air}$ is in Kelvin. In case of TT7F4, the values relate to the altitude at which the balloon burst.

In the blog posts dedicated to individual flights, I already hinted at how I actually measured the lift. First, I did a few calculations. The quantities given were the envelope and payload masses. The variable quantity was the amount of gas and consequently the ascent rate. The objective was to use as little extra lift as possible to minimize the resulting superpressure exerted on the envelope, at the same time aiming for sufficient ascent rate to overcome any undesirable weather effects. The first equation gives the resultant force of a specific amount of gas pushing the balloon up: $$F = \rho_{air}V g - m g $$ where $\rho_{air}$ is the density of air, $V$ is the volume taken up by the gas inside the balloon, $m$ is the mass of the whole system (including the mass of the lifting gas), and $g$ is the standard acceleration due to gravity. The volume of the gas at specific pressure and temperature can be calculated with this equation: $$V = \frac{m_g R_g T}{p}$$ where $m_g$ is the amount of gas in $kg$, and $R_g$ is the specific gas constant of the lifting gas (4124 in case of hydrogen). The previously acquired force was then used in the drag equation: $$v = \sqrt{\frac{2F_D}{\rho C_D A}}$$ where $F_D=F$, $\rho$ is the air density, $C_D = 0.47$ is the drag coefficient of a sphere (for simplicity), $A$ corresponds to the cross sectional area of the spherical volume taken up by the gas, and $v$ is the resultant ascent rate. With the first balloons, I chose the amount of gas to provide an initial ascent rate of 1m/s. In an attempt to ease the superpressure off even further, the lift in the last two balloons was calculated to let them start ascending at 0.75m/s and 0.7m/s respectively. The amount of free lift in kilograms, which is a quantity that can be measured during filling, can be derived from the following equation: $$m_g = \frac{(m_b+m_p+m_{fl}) \cdot p \cdot M_g}{(\rho_{air}-\rho_{g}) \cdot R \cdot T_{air}}$$ where $m_g$ is the mass of the gas, $m_b$ and $m_p$ are masses of the envelope and payload, $m_{fl}$ is the amount of free lift, $M_g$ is the molar mass of the specific lifting gas in $kg/mol$ (0.002016 in case of hydrogen), $\rho_{air}-\rho_g$ gives the difference in densities between air and the gas, $R=8.314 \, J/molK$ is the gas constant, and $T_{air}$ is the air temperature in Kelvin. At the end of these calculations, I had a specific value of free lift that would yield the desired ascent rate. I then took a weight, say 100g, tied it to the envelope and placed it on a pocket scale with sufficient resolution. Filling the balloon with hydrogen, it eventually started to rise upholding the weight. Then, when the scale read 100g - 21g (payload) - 7.5g (free lift) = 71.5g, I had the lift. I didn't have to factor in the filling hose, because I always took it out before the measurement.

A couple of images of the sealed and cut filling tube. I usually did several re-heated welds side by side from both sides to make sure.

Generally, I filled the balloons the evening prior to launch and left them in the garage overnight. In all cases, I found the lift to be 1-2g higher the next morning. The only explanation I could come up with was IR absorption that must have increased the gas temperature with respect to the surrounding air.

A curious situation came about at the launch of TT7F6W. The outside temperature was several degrees lower to the previous launches, and the sun rays didn't reach the garden for much longer as well. So it happened that the balloon standing in shade for about 45 minutes had lost almost all lift by the time I was ready to launch. Placing it in the sun saw the lift restore itself eventually and be ready for an attempt number two. A quick calculation suggests that the gas must have cooled down to be at least 7°C lower than the temperature of the surrounding air.

At the start of this section, there are two charts depicting ascent rates of all six flights up to their float altitudes. TT7F1 and F2 are recorded only to 4000m and 8000m respectively due to software/hardware issues. The data represent a 10 set average of data points mostly 1-2 minutes apart to smooth the curves somewhat. A quick look at the initial stages of individual flights suggests that the calculations outlined previously did a good enough job in sizing the lift. Worth noticing is the gradual increase in ascent rate peaking at around 10500m in case of the tube balloons. Their more aerodynamic shape causes less drag compared to the more spherical balloons allowing them to pick up speed. Another interesting curve is TT7F5's which recorded a two stage ascent forced by a layer of low clouds that held the balloon for more than two hours.

Flight	Days	Great Circle	Distance	Failure
TT7F1	8.63	8003km	9465km	indeterminable
TT7F2	2.08	2032km	3326km	failed transmitter
TT7F3	0.50	238km	275km	indeterminable
TT7F4	0.16	203km	210km	failed envelope during ascent
TT7F5	1.42	1111km	1189km	indeterminable
TT7F6	2.88	3230km	3898km	indeterminable

The table above provides a quick summary of the individual flights in terms of duration from the first received packet to the last, and in terms of the total distance between successive packets that were received. Great circle distance then represents the distance between the first and the last point on the surface of a sphere.

TT7F1 - the first and also the longest flight delivered its last packet over Japan right before it set off to cross the Pacific. It never arrived to Alaska where it was supposed to show up two and half days later. The float altitude was 500m lower (10588m) from the previous day on the last day packets were received. I didn't log the state of weather (storms, high clouds) over the Pacific at that time. A 400m wobbling in altitude was recorded at sunset of the third day.

TT7F2 - the tracker wrestled with a poor connection between the transmitter and the MCU since day one delivering the last packets on the third day over southwestern Russia. During that time, the float altitude moved between 10234m and 10524m which seems to comply with the natural range of fluctuation of a concrete pressure level within the atmosphere. I didn't log the weather conditions either.

TT7F3 - achieved the highest float altitude - 13403m. It experienced wild wobbling at sunset of the first day over Hungary. First 1100m drop in altitude followed by 800m rise and another 800m drop inside 45 minutes. It wasn't heard of the next day, nor the days after. The weather along its predicted path was clear skied and stormless.

TT7F4 - experienced an apparent envelope failure at 11864m. It was filled to a higher free lift than the previous balloon. It was also one of the latter spherical envelopes made while the impulse heat sealer was experiencing difficulties with inconsistent welding. After the failure, the balloon descended at a rate of initially -4m/s to -2m/s in the later stages. It eventually landed at the Polish-Slovak border.

TT7F5 - simply didn't show up on the third morning after two whole days without noticing any problems. The last packet was received from above the Ionian Sea. The balloon was expected to report from above Greece the next morning, but never did. After launch, the balloon was held by a layer of low clouds at about 2800m for two and a half hours before it ascended to its average float altitude of 12170m. There were no storms, nor high clouds on its predicted path.

TT7F6W - similarly to F5, both the balloon and electronics operated without any problems for the first three days. The fourth day, however, saw only one WSPR packet coming through from above Iran exactly where Hysplit had it predicted at that time. Eventually, it turned out to be the last packet, and the tracker wasn't heard of again. Over the course of the three days, the average altitude was slowly decreasing all within the range of natural pressure level fluctuation. The balloon experienced a loss of lift right before the first attempt to launch it. The lift eventually recovered after the balloon was placed in the sun. It was then successfully launched during the second attempt.

Assessing the overall envelope performance has turned out to be problematic since there was only one confirmed and recorded failure (F4). With F1's altitude drop on the last day potentially suggesting another. In case of the F3, F5 and F6 balloons, it is unclear whether their failure originated in the envelope or a broken tracker. There simply weren't any more received packets in the following days. I would think a balloon failure to be more probable during the day, around local noon or afternoon, when the lifting gas reaches the highest temperature hence the most superpressure. With respect to a nighttime failure, I can only think of loosing lift due to the gas cooling down too much with respect to the surrounding air as the possible reason. As mentioned, there were two cases of recorded wobbling in altitude as the sun set which I attribute to the gas rapidly cooling down before finding a nighttime equilibrium again.

Balloon Types Overview
This is a summary of parameters of the individual envelopes I have made. In the cases of balloons that have flown, I mention a volume figure derived from the actual float altitudes. This figure will differ in individual balloons of the same type depending on the achieved amount of stretch.

S1.33 - made of two circular pieces of film. The inner diameter of the flat shape is 1.33m (with 2cm for the circumferential welds, it corresponds to the width of the film roll), measured mass is 0.148kg and the volume derived from the actual float altitudes was 0.506m³ and 0.482m³ (dependent on the specific extent of pre-stretch).

S1.84 v1 - made of four hemispherical pieces of film. The inner diameter of the flat shape is 1.84m, measured mass is 0.283kg and the volume derived from the actual float altitude was 1.294m³ (dependent on the extent of pre-stretch). Two hemispheres are joined by a straight meridional weld, then the two resulting circular pieces are sealed by a circumferential weld.

S1.84 v2 - made of six pieces of film. The two middle shapes use the entire width of the roll - 1.35m. This is to move the welds off the highest stress area - the centre of the circular shapes. The remaining four hemispherical pieces then complete the two circular shapes 1.84m in diameter with four straight welds. A weld generally takes up about 1cm of the film. The mass of the envelope is a few grams higher than S1.84's 0.283kg due to the longer welding. The real volume is not known, because the two samples failed during pre-stretching and were never flown, but it should be comparable to S1.84's volume.

S2.66 - made of four hemispherical pieces of film. This time utilizing the full width of the roll. The inner diameter of the flat shape is 2.66m and measured mass is 0.585kg. Neither of the two samples withstood the stress on the meridional weld, so this envelope has never been launched and its volume couldn't have been derived. The construction is identical to S1.84 v1.

T2.33 - made of two pieces of film. It utilizes the full width of the roll distancing two hemispheres with a square. The length of the shape is 2.33m, the width is 1.33m, and the radius of the hemisphere is 0.665m. The mass was only calculated and adjusted by a factor derived from the real measurements of the other types to 0.287kg. The volume derived from the actual float altitude was 0.988m³. The construction requires one long circumferential weld.

T3.33 - made of two pieces of film. It utilizes the full width of the roll distancing two hemispheres with a rectangle. The length of the shape is 3.33m, the width is 1.33m, and the radius of the hemisphere is 0.665m. The mass was only calculated and adjusted by a factor derived from the real measurements of the other types to 0.427kg. The volume derived from the actual float altitude was 1.641m³. The construction requires one long circumferential weld.

Theoretical Notes
This section serves to summarize and illustrate some of the factors involved in balloon making, and the implications of different design choices. A superpressure balloon has a specific amount of lifting gas sealed inside an envelope of a specific volume. The initial ascent is due to the lifting gas causing buoyant force in upward direction that is bigger than the weight of the whole system. The amount of 'free lift' decides the ascent rate. As the balloon ascends, the surrounding air pressure decreases allowing the gas to expand decreasing the density of the whole system and keeping it lower than the density of the surrounding air. At some point, the expanding gas fills the whole envelope after which the buoyant force gradually decreases while the balloon still ascends. The floating phase starts when the buoyant force equals the weight of the whole system, in other words the system's density is in equilibrium with the density of the surrounding air. The difference in pressure levels between the point the gas stops expanding and the moment the balloon no longer ascends corresponds to the extent to which the envelope gets pressurized and is referred to as superpressure. On top of that, the envelope is subjected to variations in temperature of the lifting gas with respect to the temperature of the surrounding air. This is referred to as supertemperature and may further add to the pressure inside the envelope. The pressurized vessel is then subjected to stresses inside the envelope material.

For the sake of simplicity I will be using a perfect sphere defined by its radius to represent the balloons in the following examples.

One of the advantages of a spherical envelope is that the tensile stress is the same at any point around the surface in both the x and y directions. The equation to compute the circumferential stress is: $$\sigma = \frac{pr}{2t}$$ where $p$ is the balloon's internal superpressure, $r$ is the radius of the sphere, and $t$ is the envelope thickness.

In the first blog post on superpressure balloons, I misunderstood some of the concepts taking place. The following, hopefully, clears up the confusion. The above is a chart of four stress-strain curves of Mylar taken from DuPont's Physical-Thermal Properties datasheet. I chose Mylar to use in some of these examples for the amount of data openly available as opposed to other balloon materials. Tensile stress is a force per unit area causing tensile strain, an amount of deformation expressed as a ratio of the extension to the original length. In terms of a balloon, it's the force trying to rip the walls apart as indicated in the illustrations above. As mentioned previously, a spherical envelope is subjected to uniform stresses in all directions. The behaviour described by the stress-strain curve could be divided into two regions. First, the elastic region which encompasses the stresses a material can take and still return to its original size and shape when the stress is removed. The proportional limit within this region demarks the point after which the ratio of stress to strain is no longer proportional. The ratio inside the initial linear region itself can be found in datasheets as the Young's modulus and gives a quick estimate of how stiff the material is (how much it resists deformation). Based on the Mylar curves, this occurs around 2-3% elongation (though the original chart doesn't provide very good resolution). The elastic limit of a material indicates the end of the elastic region and the beginning of the plastic region with stresses that lead to permanent deformation. The yield point is defined as the first stress at which an increase in strain occurs without an increase in stress. In case of the Mylar curves, this seems to happen at around 13-16% elongation. The behaviour outlined by the mentioned limits and points (and their existence as a matter of fact) is dependent on the type of material (polymer, metal, etc.) and specific temperature in question. A polymeric material at very low temperatures (below their brittle-ductile transition temperature: LLDPE -70°C, PA 66 -80°C for example) becomes brittle and breaks without any plastic deformation. The chart above describes the behaviour of a Mylar film at four different temperatures in a range a balloon envelope is likely to encounter (all below the glass transition temperature of Mylar: 73-80°C). At 35°C, a slightly hotter room temperature, the material plastically deforms and breaks at lower stress but much higher strain. At lower temperatures (-55°C and -70°C), the material becomes tougher (toughness defined as the energy per unit volume a material can absorb before rupturing) and stiffer, and breaks at much higher stress but less elongation. An interesting actuality in polymer materials is that the same effects caused by varying the temperature can be achieved by varying the strain rate. Keeping temperature constant and increasing the strain rate leads to the material behaving tougher and stiffer while slower strain rate leads to the opposite effect. A change in temperature is indistinguishable from a change in strain rate. This principle manifests itself as creep. At constant temperature, a material under permanent stress continues to slowly deform until the stress is relieved or the material fails. Given the nature of a superpressure balloon, that is constantly pressurized hence in permanent stress, the material creep puts a finite limit on the envelope's operating life. However, at least the low temperatures at which it operates and the regular nighttime drops in superpressure slow down the creep rate.

r (m)	V (m3)	t (μm)	p (Pa)	σ (MPa)
0.25	0.065	50	1000	2.50
0.50	0.524	50	1000	5.00
0.75	1.767	50	1000	7.50
1.00	4.189	50	1000	10.00

The table above shows how the tensile stress in an envelope depends on the radius of the balloon. At the same superpressure, the walls of a larger envelope are subjected to higher stress. This is noticeable particularly during stretching and needs to be taken into account when planning a stretching profile. For example, the smaller S1.33 envelopes were stretched with gauge pressures of up to 2.2-2.3kPa while the larger S1.84 envelopes only up to 1.5-1.7kPa. I also saw weld failures in the largest S2.66 envelopes as early as 400Pa.

r (m)	V (m3)	mb (kg)	mp (kg)	mg (kg)	v (m/s)	mfl (kg)	alt (m)	sp (Pa)	σ (MPa)
0.25	0.065	0.038	0.010	0.00396	1.0	0.0046	4240	5237	13.1
0.50	0.524	0.153	0.010	0.01297	1.0	0.0101	11492	1201	6.0
0.75	1.767	0.345	0.010	0.02780	1.0	0.0168	14288	593	4.4
1.00	4.189	0.613	0.010	0.04842	1.0	0.0244	16193	361	3.6

On the other hand, lifting the same payload (10g) with the same initial ascent rate (1m/s) with larger envelopes leads to less superpressure inside the balloon and less stress in the material. These calculations assume the temperature of the gas (hydrogen) and ambient air to be the same, and do not account for the effect of supertemperature which depends on altitude (more on that later).

r (m)	r/r	V (m3)	V/V	m (kg)	m/m	ρ (kg/m3)	ρ/ρ	alt (m)	a/a
0.25		0.065		0.038		0.5856		7059
0.50	2	0.524	8	0.153	4	0.2928	0.5	12377	1.75
1.00	2	4.189	8	0.613	4	0.1464	0.5	16770	1.36
2.00	2	33.510	8	2.453	4	0.0732	0.5	21139	1.26
4.00	2	268.083	8	9.812	4	0.0366	0.5	25475	1.21
8.00	2	2144.661	8	39.247	4	0.0183	0.5	29897	1.17

This table points out the relationship between the balloon's radius and its float altitude. Using the same material (50μm 976kg/m³ dense PE/PA/EVOH/PA/PE film) and doubling the radius leads to increasing the volume 8 times, increasing the mass 4 times, and consequently more or less halving the system density (mass of the additional gas required offsets this a little). The air pressure, however, decreases much faster with altitude. This puts a practical limit on reaching higher altitudes by increasing the balloon's radius. The density-altitude values are based on the U.S. Standard Atmosphere model.

material	t (μm)	ρ (kg/m3)	r (m)	V (m3)	mb (kg)	mg (kg)	alt (m)	sp (Pa)	σ (MPa)
S1.84 (TT7F3)	50	976		1.237	0.283	0.02302	13241	745
PE/PA/EVOH/PA/PE	50	976	0.666	1.237	0.272	0.02217	13485	726	4.8
PE/PA/EVOH/PA/PE	40	976	0.666	1.237	0.218	0.01796	14842	632	5.3
MYLAR	50	1390	0.666	1.237	0.387	0.03107	11314	910	6.1
MYLAR	36	1390	0.666	1.237	0.279	0.02270	13332	738	6.8
MYLAR	25.4	1390	0.666	1.237	0.197	0.01634	15449	593	7.8
MYLAR	12.7	1390	0.666	1.237	0.098	0.00868	19537	389	10.2
HEPTAX	25.4	953	0.666	1.237	0.135	0.01154	17699	470	6.2

In light of this, a more reasonable way to increase altitude is using thinner or less dense materials. The table compares the performance of TT7F3's envelope with seven other idealized spherical balloons made of available materials with different thicknesses and densities. The envelope volume, the payload mass (10g), and the initial ascent rate (1m/s) were set the same in all cases. As is apparent, it is the envelope mass that changes, leads to less required gas, and consequently higher altitudes. The superpressure inside the envelope also decreases, however, since the cross sectional area exposed to the tensile forces shrinks, the stress in the material actually increases.

These two charts examine the effect of increasing payload mass with respect to the mass of the envelope for three different spherical balloons. All data points were computed with the initial ascent rate set to 1m/s. The actual payload masses range from 0 to 50g in 5g increments. Increasing payload mass leads to lowering the float altitude and increasing stress in the envelope. In absolute terms, it's apparent that smaller balloons are affected more since the payload represents larger portion of the overall mass.

The two images show an S1.33 envelope first at slightly above 0Pa of internal pressure, then after hours of stretching at more than 2kPa. There are three reasons for pressurizing newly manufactured balloons. First, to verify that the envelope was properly sealed and that the welds hold at expected stresses. I consider this mandatory. Second, to relieve localized stress concentrations in the welds and the film itself. This is highly recommended. And the third reason is optional and consists of carrying on the plastic deformations to further increase the envelope's volume.

Practically, the weld testing could be done by rapid inflation which has, in terms of the stress-strain curves, the same effect as lowering temperature. In other words, high internal pressure and consequently stress in the material lead to very little elongation and plastic deformation. The stress relieving, on the other hand, requires the material to deform plastically. The envelope is pressurized very slowly at room temperature which means that significant elongation can be achieved at relatively low stresses. The spots with concentrated stress elongate first evening the local stress with the surrounding levels. This is apparent from the shape of the envelope slowly progressing towards an ideal sphere where stress is uniformly distributed along the whole surface. In terms of the welds, the initial wrinkles get slowly smoothed out.

One consequence brought about by stretching is that the material gets thinner. To calculate the negative strain in the z dimension, it is necessary to take into account the stress in x and y directions as in the following equation: $$ \varepsilon_z = - \nu (\sigma_x + \sigma_y) / E$$ still working with idealized spheres in these examples, $\sigma_x$ and $\sigma_y$ are equal, $\nu$ is the Poisson's ratio which for Mylar is 0.38 in the elastic region and 0.58 in the plastic region, and $E$ is the Young's modulus (3447MPa for Mylar). Now, I am not certain whether this equation can be used for calculations in the plastic region as well. Nevertheless, the following example computes $E$ in the plastic region simply as $\sigma / \varepsilon$ for each data point (all values extracted from the 35°C stress-strain curve). Hopefully, it can produce a rough approximation of the effect of stretching without introducing too much error.

material	r (m)	mb (kg)	mg (kg)	V0 (m3)	t0 (μm)	alt0 (m)	σ0 (MPa)	sp0 (Pa)
MYLAR	0.5	0.055	0.00531	0.524	12.7	17277	13.1	9876
MYLAR	0.5	0.111	0.00966	0.524	25.4	13394	9.7	19751
MYLAR	0.5	0.157	0.01327	0.524	36	11343	8.5	27994
MYLAR	0.5	0.218	0.01801	0.524	50	8926	7.9	38880

ε1 (%)	V1 (m3)	t1 (μm)	alt1 (m)	σ1 (MPa)	sp1 (Pa)	ε2 (%)	V2 (m3)	t2 (μm)	alt2 (m)	σ2 (MPa)	sp2 (Pa)
10	0.697	11.2	19089	12.2	7936	20	0.905	9.8	20729	11.7	6320
10	0.697	22.5	15206	9.1	15873	20	0.905	19.5	16861	8.8	12641
10	0.697	31.8	13155	7.9	22497	20	0.905	27.6	14810	7.7	17916
10	0.697	44.2	11183	7.0	31245	20	0.905	38.4	12838	6.8	24883

Four same size different thickness Mylar balloons in a shape of an ideal sphere were modelled at 0%, 10% and 20% stretch all lifting 10g payloads at 1m/s initial ascent rate. The $\sigma$ parameter represents the stress due to superpressure from the required lifting gas at float altitude while the $sp$ parameter represents the maximum internal pressure the envelope can sustain at -55°C (corresponds to 194.4MPa breaking stress). As the envelope stretches, the float altitude increases and stress in the material due to the lifting gas decreases despite the decreasing wall thickness. However, the maximum sustainable superpressure decreases as well. That is because the envelope's radius increases with the volume which means that the same internal pressure level leads to higher stress. From a practical point of view, it should be noted that stretching Mylar, due to its strength, requires machinery capable of generating and sustaining much higher pressure levels than when stretching the PE/PA/EVOH/PA/PE film.

balloon	V (m3)	m (kg)	V/m	rs (m)	Vs (m3)	ms (kg)	Vs/ms	V/Vs
S1.33 (TT7F1)	0.476	0.148	3.22	0.491	0.496	0.148	3.35	96.0%
S1.33 (TT7F2)	0.455	0.148	3.07	0.491	0.496	0.148	3.35	91.8%
S1.84 (TT7F3)	1.237	0.283	4.37	0.679	1.311	0.283	4.64	94.3%
T2.33 (TT7F6)	0.988	0.287	3.44	0.684	1.340	0.287	4.67	73.7%
T3.33 (TT7F5)	1.641	0.427	3.84	0.834	2.430	0.427	5.70	67.5%

A useful way of quickly comparing envelopes of different shapes and materials is their Volume to Mass ratio. The table above provides these ratios for five of the TT7F envelopes. Further, it compares them with ratios of ideal spheres made of the same material of equivalent mass. The last column then shows how close I got to the ideal shape of a sphere with individual envelopes. Ideal in terms of maximizing internal volume per mass of material. A comparison of F3 and F5 illustrates that envelope shape is crucial, and despite weighing 1.5x more, F5 eventually floated 1200m lower than F3 as anticipated by the ratio. The reciprocal of the V/m ratio is basically a density level corresponding to an altitude at which the envelope would float if it could hold the 'inflated' shape with vacuum inside. It can be viewed as an upper limit which the balloon won't surpass.

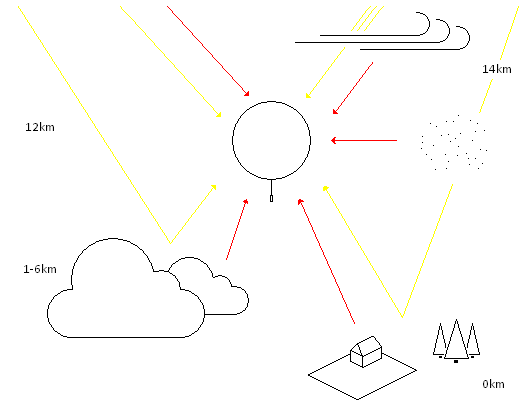
The following few paragraphs address the balloon's radiation environment and supertemperature. During the day, the envelope is exposed to the Sun's radiation arriving on Earth. Upon hitting the material, a portion of the rays is reflected, a portion is absorbed and the remainder is transmitted through the material. The sizes of the portions are dependent on a specific wavelength and the material's properties. Given the geometry of a balloon, three separate interactions between the rays and the walls of the balloon should be taken into account. First, the full radiation arrives at the outer surface of the envelope (the rays see a circular cross-sectional area). Then the transmitted portion interacts with the inner surface on the other side of the balloon. And finally, the reflected portion from the second interaction hits the material from the inside of the balloon once more. Beyond the third interaction the remaining radiation still to be absorbed is negligible.

In Dupont's Optical Properties datasheet, I found a transmittance curve of 23 micron thick transparent Mylar 92D film covering a range of 0.2 to 50μm wavelengths. The curve shows that about 85% of the incident power in the visible spectrum (390-700nm) is transmitted through the material. The remaining power is split between absorption and reflection. Unfortunately, the datasheet nor the Internet provide any reflectance or absorption curves. Worth noting is that higher up in wavelength the material is much less transparent to the infrared radiation and absorbs or reflects substantial percentage of the radiation.

For the sake of this example, I will assume a hypothetical material based on the Mylar 92D's transmittance and constant 4% reflectance throughout the whole spectrum. The orange curve in the chart above corresponds to a blackbody radiation of the Sun (5505°C) after travelling 149.6 million kilometres to the top of the Earth's atmosphere (1366W/m² of total power). The light blue curve then maps the power absorbed per square meter by the material per individual wavelength (163.5W/m² in total). The second chart represents a blackbody radiation of an object at -55°C (to illustrate an envelope at float altitude) under the red curve (126.5W/m²). Based on the Kirchhoff's law of thermal radiation which states that at thermal equilibrium the emissivity is equal to the absorptivity, the dark blue curve outlines the power actually emitted by the envelope's material per square meter (50.8W/m²). Note the logarithmic scale of the x axes and two orders of magnitude difference between the y axes.

To paint the full thermal radiation picture of a balloon floating at 12km altitude, a couple more contributors need to be taken into account. Aside from the direct solar radiation, the balloon may face reflected solar radiation from a continuous cloud cover below. In Lally, Vincent E. Superpressure Balloons for Horizontal Soundings of the Atmosphere. NCAR, 1967, it is stated that this reflection could be as high as 800W/m². Another factor impacting the solar radiation is a potential presence of cirrus clouds above the balloon. Lally again states that at this altitude the cirrus clouds rarely reduce the radiation by more than 10%. Aside from reflecting solar radiation, both the above and below clouds contribute by radiating in infrared based on the temperature at the base of the higher cloud and the temperature at the top of the lower cloud (approximated by blackbody radiation at the given temperatures). In case of clear skies, the balloon faces thermal radiation from the ground (I repeatedly came across an averaged value of 240W/m², Lally offers altitude dependent range of 150-450W/m²) and the remaining air mass above (Lally provides an estimate of 20W/m² at this altitude - corresponding to blackbody radiation of a body at -136°C). Solar radiation reflected off the ground is usually stated to be 4%. The remaining radiation contribution comes from the sides of the balloon, and according to Lally can be approximated to a blackbody radiation at the temperature of the surrounding air (129W/m² at -55°C).

I used this tool, which provides raw data per wavelength for download, to generate the blackbody radiation curves. Alternatively, the Stefan-Boltzmann law can be used to get the total power radiated by a black body at a specific temperature: $$ P = \varepsilon \sigma A T^4$$ where $P$ is the total power radiated by a black body at temperature $T$ (kelvin), $\varepsilon$ is emissivity in case the body emits less than the idealized black body, $\sigma = 5.67 \times 10^{-8} \: W \cdot m^{-2} \cdot K^{-4}$ is the Stefan-Boltzmann constant, and $A$ is the area of the radiating surface.

CLEAR DAY	Pt (W/m2)	Pa (W/m2)	absorbed	contribution
direct solar	1366.0	307.0	22.5%	44.7%
ground reflected solar (4%)	54.6	12.3	22.5%	1.8%
ground emitted IR	240.0	171.2	71.3%	24.9%
atm. emitted IR - sides (-55°C)	129.0	90.9	70.5%	26.5%
atm. emitted IR - above (at 12km)	20.0	14.4	72.0%	2.1%
thermal equilibrium	9.7°C	2157.8W		100.0%

The table above summarizes a potential scenario which a balloon floating at 12km altitude may experience during a cloudless day. The second column contains radiation flux estimates per individual contributor. The actual power absorbed during the three interactions described earlier (outside surface absorption, opposite inner surface absorption and absorption from the second reflection) is in the third column. All values reflect the material's absorptivity at each individual wavelength. $$ P = \Phi_1 \pi r^2 + \Phi_2 \pi r^2 + \Phi_3 \pi r^2 + 2 \Phi_4 \pi r^2 + \Phi_5 \pi r^2$$ The total absorbed power by a balloon with 1 meter radius made of the hypothetical material is 2157.8W. All contributors were multiplied by the balloon's cross-sectional area and summed. Note the larger area in case of the side flux $\Phi_4$. $$ T = \sqrt[\leftroot{1}\uproot{2}\scriptstyle 4]{\frac{P}{\varepsilon \sigma (4 \pi r^2)}} $$ The equation above computes the temperature of the film after the balloon reaches thermal equilibrium. In other words, it reaches a temperature at which it emits as much power as it absorbs. The area, in this case, is the whole surface of the sphere, and $\varepsilon = 0.47$ is an averaged emissivity of the material in infrared. The calculated film temperature due to radiation in this particular scenario rose to 9.7°C with the surrounding air at -55°C. Assuming the gas inside the balloon reaches thermal equilibrium with the film, the envelope is exposed to stresses caused by 64.7°C of supertemperature. In reality, the actual film temperature would be somewhere between this upper limit and the ambient air temperature, because of air conduction and convection taking some of the heat away. These effects, though, seem quite complex to estimate any closer.

CLEAR NIGHT	Pt (W/m2)	Pa (W/m2)	absorbed	contribution
ground emitted IR	152.0	107.4	70.7%	35.4%
atm. emitted IR - sides (-55°C)	129.0	90.9	70.5%	59.9%
atm. emitted IR - above (at 12km)	20.0	14.4	72.0%	4.7%
thermal equilibrium	-42.5°C	953.8W		100.0%

Another scenario is a cloudless night. Aside from omitting the solar radiation, the ground emitted infrared radiation was decreased to the lower limit provided by Lally to examine a more extreme situation. This time the upper limit for the film temperature fell to -42.5°C, still 12.5°C above the ambient air temperature.

CLOUDY DAY	Pt (W/m2)	Pa (W/m2)	absorbed	contribution
direct solar (10% cirrus reduction)	1229.4	276.4	22.5%	27.5%
lower clouds reflected solar	720.0	161.9	22.5%	16.1%
lower clouds emitted IR (5°C)	340.0	246.4	72.5%	24.5%
upper clouds emitted IR (-30°C)	198.0	139.5	70.5%	13.8%
atm. emitted IR - sides (-55°C)	129.0	90.9	70.5%	18.1%
thermal equilibrium	38.0°C	3160.5W		100.0%

A scenario with a continuous cloud cover underneath the balloon and a presence of high cirrus clouds seems to be among the more demanding conditions to encounter. Particularly due to the additional solar reflection and more prominent contribution from above in the form of a much warmer IR emitter than was the clear sky in the first example. This time the upper limit for supertemperature rose as high as 93°C.

CLOUDY NIGHT	Pt (W/m2)	Pa (W/m2)	absorbed	contribution
lower clouds emitted IR (5°C)	340.0	246.4	72.5%	43.4%
upper clouds emitted IR (-30°C)	198.0	139.5	70.5%	24.6%
atm. emitted IR - sides (-55°C)	129.0	90.9	70.5%	32.0%
thermal equilibrium	-3.5°C	1783.5W		100.0%

During a cloudy night the balloon would also operate quite pressurized with the upper limit at 51.5°C of supertemperature. All the radiation flux values used in these scenarios represent only a limited collection of examples for illustratory purposes. Reality provides a much wider spectrum of situations. The radiation analysis also highlights my previous misunderstanding of Table 9 in Lally, Vincent E. Superpressure Balloons for Horizontal Soundings of the Atmosphere. NCAR, 1967 which provides maximum daytime temperature increase values for different altitudes. I originally considered those to be the total supertemperature not realizing the balloon wasn't at thermal equilibrium with the ambient air during the night.

scenario	Mylar 92D	metallized	high ε in IR
clear day	9.7°C	173.7°C	-30.4°C
clear night	-42.5°C	-64.5°C	-61.3°C
cloudy day	38.0°C	211.3°C	-5.1°C
cloudy night	-3.5°C	-29.8°C	-26.1°C

This table compares three materials of different absorptivity, reflectivity and transmittivity in a context of the previous four scenarios. First is the hypothetical Mylar 92D based material with averaged absorptivity in visible wavelengths $\alpha_{vis} = 0.12$, averaged absorptivity in infrared $\alpha_{ir} = 0.47$, and averaged emissivity in infrared $\varepsilon_{ir} = 0.47$. The second material represents a metallized, highly reflective film both in visible and infrared - $\alpha_{vis} = 0.06 $, $ \alpha_{ir} = 0.01 $, $ \varepsilon_{ir} = 0.01$. The problem with these surfaces is that they are poor emitters which leads to extreme heating during the day. The envelope has to reach temperatures in range of 200°C to be able to radiate as much power as it absorbs. The third case is an example of a hypothetical material relatively transparent in visible wavelengths and highly emissive in infrared - $\alpha_{vis} = 0.08 $, $ \alpha_{ir} = 0.90 $, $ \varepsilon_{ir} = 0.90$. The high emissivity allows the film to stay relatively close to the ambient temperature (-55°C). However, in the case of the clear night scenario, it could lead to cooling the gas below ambient temperature (supertemperature of -6.3°C) decreasing its lift, and potentially bringing the balloon down.

r (m)	spfl (Pa)	sp64.7 (Pa)	σ (MPa)	sp12.5 (Pa)	σ (MPa)	sp93.0 (Pa)	σ (MPa)	sp51.5 (Pa)	σ (MPa)
0.25	3955	15794	85.8	6243	33.9	20973	114.0	13379	72.7
0.50	931	5438	59.1	1802	19.6	7409	80.5	4518	49.1
0.75	453	3262	53.2	996	16.2	4491	73.2	2689	43.8
1.00	275	2324	50.5	671	14.6	3221	70.0	1906	41.4

This table summarizes the effect of supertemperature on superpressure and consequently on stress in the material. Four sizes of an idealized sphere made of the hypothetical 23μm Mylar 92D material were confronted with the upper limits for supertemperature from the previous four scenarios. They were modelled as lifting 10g payload at initial ascent rate of 1m/s. The second column holds the amounts of superpressure experienced by individual balloons only due to the free lift (the excess amount of gas). The following columns then address the superpressure and stress values at the marked supertemperature levels (ambient air -55°C, film temperature 9.7°C, supertemperature 64.7°C).

r (m)	V (m3)	mg (kg)	Alt. (m)	P (Pa)	T (°C)	ST (°C)
0.25	0.065	0.00290	7131	40289	-31.4	-21.6
0.50	0.524	0.00884	13968	14159	-56.5	-13.4
0.75	1.767	0.01861	16872	8954	-56.5	-10.4
1.00	4.189	0.03217	18818	6587	-56.5	-8.7

As long as a balloon is pressurized, the density of the system stays the same (ignoring any potential stretching of the envelope due to stress), and the balloon floats along the same air density level. If, however, the lifting gas cools down with respect to the air temperature, the pressure inside the balloon will decrease. Below a certain temperature the weight of the system becomes higher than the upward force generated by the gas, and the balloon starts to descend. It will keep descending as long as the supertemperature stays below this limit. If the temperature of the gas rises above the limit, the balloon will ascend back to its float altitude. The amount of supertemperature, positive or negative, then determines the ascent/descent rate. $$ T_g = \frac{ V P}{m_g R_g} $$ This equation, where $R_g = 4124 \: J \cdot kg^{-1} \cdot K^{-1}$ for hydrogen, gives the absolute temperature of the limit in kelvin. The table above illustrates these limits for four different sizes of balloons (1m/s initial ascent rate, 10g payload). The pressure and temperature columns correspond to standard atmosphere model at respective float altitude. The last column then represents the amount of negative supertemperature at which the balloon starts to descend. In other words, the temperature of the gas must be more than 21.6°C below the air temperature (-31.4°C) in case of the smallest balloon.

Another factor limiting a superpressure balloon's lifetime is gas loss due to diffusion through the material. Datasheets often provide permeability figures of the material for different gases. In case of a balloon, there is a limiting amount of gas lost after which the balloon loses its lift and descends. It can be estimated for different envelope sizes with this equation: $$ \% \: Gas \: Loss \: = \frac{m_{fl}}{m_{fl}+m_b+m_p} \cdot 100$$ where $m_{fl}$ represents the free lift, $m_b$ is the balloon mass, and $m_p$ is the mass of the payload. The resulting percentage then represents the fraction of $m_g$, the actual mass of the gas in kilograms, the balloon can lose before it starts to descend.

Material	Thick.	Conditions	O2	He	H2
Mylar	23μm	25°C	76.0	2229	1521
Heptax	25μm	20°C 60%RH	6.9	800
PE/EVOH/PE	40μm	23°C 50%RH	3.5
PE/PA/EVOH/PA/PE	50μm	23°C 0%RH	2.8

The most frequent figure I came across is a material's permeability to oxygen which isn't much of a use in actual balloon's operating life estimate, but it may at least indicate how it compares to other materials as a general gas barrier. Some sources, luckily, provide hydrogen and helium permeability figures as well. The table above contains these converted to common units of $cm^3 \cdot m^{-2} \cdot atm^{-1} \cdot day^{-1}$. The figures slightly differ in conditions at which they are said they were measured. According to Lally, permeability decreases with temperature. He then provides a table of measured Mylar permeabilities to helium at a wide range of temperatures (Table 3 in Superpressure Balloons for Horizontal Soundings of the Atmosphere). $$ Rate\,of\,loss\,= \frac{\delta p A}{t}$$ this equation computes the amount of gas in $cm^3$ that diffuses through an area $A$ per day. The permeability of the material is specified by $\delta$, $p$ then represents the partial pressure of the gas across the film, and $t$ is the film thickness.

As an example, I tried to model three different 23μm Mylar envelopes lifting 10g payloads at 1m/s initial ascent rate, this time, filled with helium. The envelopes were spheres with radii of 0.50m (blue), 0.75m (orange) and 1.00m (green). An average supertemperature over the balloon's lifetime of 45°C was assumed (-56.5°C ambient air) giving permeability of 680cm³m^-2atm^-1day^-1 (Lally). Partial pressure was assumed to be the pressure exerted by the amount of helium at supertemperature on the volume of inflated envelope. The operating life of the smallest balloon reached 83 days, the mid one lasted 152 days, and the largest envelope descended after 229 days. The whole code is in this Jupyter notebook.

In the second example, I kept the envelope sizes the same (0.524m³) and varied the average supertemperature and consequently the permeability. The blue line represents 45°C of supertemperature with 680cm³m^-2atm^-1day^-1 of diffused gas, the orange 25°C with 280cm³m^-2atm^-1day^-1, and the green line 0°C with 80cm³m^-2atm^-1day^-1. Cooling down the envelope saw the operating life increase from 83 days to 855 days with 218 days for the mid values.

The permeability's dependence on temperature seems to be the dominant factor in slowing down the diffusion. This should favour transparent, highly emissive films in infrared over metallized envelopes. Further, larger balloons are advantageous from two standpoints. The amount of gas lost per day constitutes a smaller fraction of the total amount of gas. And the partial pressure of the lifting gas is lower than in a smaller envelope. This section dealt with gas diffusion through the material only. Gas loss may be further intensified due to microleaks - microscopic holes in the material.

	Mylar 92A	Heptax	TR9	TR9	TRB40
Thickness (μm)	23	25	40	50	40
Density (kg/m3)	1390	953	972	976	945
Tensile Strength (MPa) - TD	234	100	30	30	22
Tensile Strength (MPa) - MD	200	102	26	26	18
Elongation at Break (%) - TD	91	90	400	400	400
Elongation at Break (%) - MD	116	153	450	450	400
Modulus (MPa) - TD	5102
Modulus (MPa) - MD	3378
Poission's Ratio (before yield)	0.38
Poission's Ratio (after yield)	0.58
Thermal Weldability (°C)			125-160	125-160	120-160
Melt Point (°C)	254
Haze (%)	16	3
Transmittance (visible)	0.9
OTR (cm3m-2atm-1day-1)	76.0	6.9	2.5-3.0	2.5-3.0	3.0-4.0
He perm. (cm3m-2atm-1day-1)	2229	800
H perm. (cm3m-2atm-1day-1)	1521

This table contains specifications of several films for comparison. I haven't managed to obtain all the data for all the films. TR9 is the 50μm PE/PA/EVOH/PA/PE film I used on TT7F balloons. TRB40 is a PE/EVOH/PE material I started with when making balloons, but I've never actually launched any of those. Mylar 92A is one of a wide range of BoPETs - biaxially-oriented polyethylene terephthalates. Other Mylar types, aside from a number of thicknesses, offer different degrees of haze, or the possibility of a metallized finish. Apparently, not all Mylar films are heat sealable. Heptax is said to be a clear 7-layered film coextruded from nylon, EVOH and LLDPE that has been successfully used on balloons and blimps.

Another referenced potential cause of superpressure balloon failure is the accumulation of ice on the envelope. Too much icing negatively impacts the total mass of the system and may lead to loss of lift. At target altitudes above 10km, balloons don't encounter that many clouds, thus the main threat lies in the ascent portion of the flight. The simplest way to limit potential sources of icing is choosing the right conditions to launch, ideally clear skies.

All the previous examples assumed idealized spheres for the modelled balloons. In reality, however, the inflated shapes aren't spherical and stress isn't distributed evenly. Depending on the actual shape, the material is at some places stressed and deformed more than the idealized computation suggests, and this needs to be taken into account. Balloons made of two circular pieces of film are stressed the most in the centre of the circular shapes while the circumferential weld rests along a relatively unstrained spot. In case of the tube, or cylindrical shaped balloon, the main stress is concentrated in the middle of the body with the welds being stressed slightly less than the centre of the piece of film.

In light of the TT7F flights, I would say that to better assess an envelope's performance, it would be preferable to design a simple low power tracker that runs on a primary cell (non-rechargeable, e.g., Li-FeS₂). The lifetime would be limited, but the primary cell's superior low temperature performance could provide an overnight coverage of the balloon's behaviour.

Practical Notes
Over the course of making the balloons, I encountered several issues. Mainly because of the heat sealer I used. The following paragraphs describe what I dealt with.

One of the issues was that the heat sealer kept overheating. It takes quite a lot of individual welds to make the whole balloon. Especially, if you want to make the welds properly. The device eventually warms up so much that it's hard to rest your fingers on it when positioning the film. Also, the welds start to warp and stick together. In the end, I adopted a practice of welding for 10-15 minutes, then waiting for the heat sealer to cool down for about half an hour before continuing again. This way, it took me about 5 hours to make S1.33 (13h - S1.84, 8.5h - T2.33, and 11.5h - T3.33), including cutting out the shapes, but excluding stretching.

Making cardboard templates first speeds up the process a lot. It also helps with ensuring the resulting shape is as uniform as possible. Irregularities in the shape lead to uneven stress distribution.

Doing the circumferential welds isn't usually a problem. The length of a single weld fits easily inside the heat sealer, and it could probably be done even with a shorter device. There would simply be more individual welds at a larger angle between them.

However, in case of long straight welds, the length of the heat sealer isn't sufficient, and they have to be done length after length. The problem is that my heat sealer has a fixed arm at one end, so the film has to be bent out of the way. A long straight weld then has to be made by bending and overlapping as in the image above.

Another aspect to welding is the strength of the weld. The heat sealer I use allows setting the duration for which it works, but the maximum is only about 3.5s which doesn't produce sufficient welds. After a lot of experimentation, I eventually settled on reinforcing the weld by immediately doing it again. Then doing another weld right next to it in the same way. And finishing it with one weld from the other side. Also heated twice in succession. The last two tube balloons were made this way, and I didn't notice any weld openings during their stretching.

These images capture the state of the end of the weld when making long straight welds. At first, it is fine, but as the machinery heats up, the ending gets more and more deformed and outstretched. In extremity, the film gets burned through or tears as it is pulled off the heat sealer.

To avoid this, I began to use a small wooden tablet to pad the overlapping film, so it doesn't touch the hot parts beyond the end of the pressing arm.

The filling tube, as shown in the image above, is particularly sensitive to proper weld endings due to its shape. In one case, before I noticed this behaviour, I had finished the hole balloon only to find out I couldn't fill it, because the filling tube had been sealed.

During the period in which I had major issues with weld openings, I tried to use test stripes every few welds to regularly check the weld quality. However, it turned out to be insufficient to identify weakening of the heat sealer's performance early enough.

This is the instrument I used to make all six balloons that were launched. It is a common impulse heat sealer marked as FS-300. Although, I bought it in the Czech Republic for about €59, I reckon it's identical to what the Chinese sellers offer on Ebay. The length of the wire is 30cm, but there are longer and shorter models on the market.

The main problem with this machine comes from the way the heating wire is attached to the rest of the circuit. As I had been using the heat sealer for a while, and quite extensively, the connection between the two wore out, it began to arc occasionally, and the weld quality became inconsistent.

After looking into it a bit closer, I found the ring connection to be completely oxidised. Measuring the resistance between the oxidised ring and the other side of the wire showed readings in tens even hundreds of ohms. A brand new wire is supposed to have resistance of 2Ω. This would explain the inconsistency in produced welds. As resistance of the circuit rises, less current flows through the wire, and it doesn't heat up enough. Filing off the deposit saw the resistance fall back down to reasonable values.

To improve the contact between the ring and the connector, I stuffed in a piece of a nail and secured it in with another piece of metal. This seemed to have stopped the arcing.

I also covered the other connector with additional teflon tape since it comes in contact with the film. It doesn't stop the heat, but it is sufficient to prevent from accidentally burning through the film.

Over the course of several failed envelopes, I attempted a continual cycle of filing of the ring connections and regularly checking the weld quality with test stripes. But eventually, I gave up and bought a new 4mm heating wire with a teflon strip which was quite pricey. Basically, a third the cost of a new heat sealer. After replacing the wire and adopting the double weld on top, single weld on the bottom, both done twice technique, I managed to make the two tube balloons. Both without any signs of weld openings.

These are the insides of the impulse heat sealer. The cheapness is apparent at first sight. At one point, the connector for the heating wire disappeared inside the device, I then had to open it up and reinforce the whole structure with an additional screw.

I wondered about how Qualatex do their welding on the 36" party balloons they sell. I then came across several Youtube videos showing the machines that do the mass production of foil balloons. From those, it seemed there was a form for the whole balloon shape that does all the welds at once and cuts the whole shape out at the same time. Based on that people have flown these balloons around the world, it probably produces consistent and reliable welds, but it is limited in the maximum balloon size by the machine's dimensions.

Having undergone ordeal with the impulse heat sealer, and knowing about people having a go at constructing custom sealing machines, I thought about how I picture a homemade device. Ideally, it would allow the film to continue beyond both ends of the wire without bending. Meaning, the hinge of the pressing arm would be parallel to the wire. The length of the heating element would probably depend on intended balloon shape and size, but generally with the possibility of easily doing welds length after length it wouldn't have to be any longer then the 30cm of the impulse heat sealer. The width of the wire ideally towards 10mm, so doing single weld is enough. The heating time could be derived from testing for a specific film. Heat dissipation may be an issue as it is on the impulse heat sealer. What I would like to add is some form of feedback on the weld quality. Perhaps sampling the current running through the circuit, or a thermocouple on the heating wire to provide a weld to weld comparison.