The Balloon

After weighting the payload, I gained a figure important for further calculations. The principle behind the balloon's flight is simple. The balloon gets filled with helium. Helium at the same pressure has lesser density than air, thus applying upward directed force on the balloon. As the balloon ascends, the air pressure decreases allowing the balloon to expand. The helium within the balloon expands as well, and thus its density decreases too. With this happening throughout the ascent, the balloon keeps its buoyancy. The limit for this cycle is the balloons ability to expand. Each balloon has a specified burst diameter. After reaching this limit, the balloon bursts and the payload falls back to the earth slowed down by the parachute.

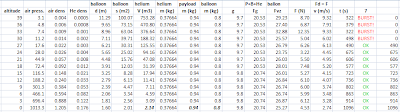
Since I wanted the balloon to reach 30 kilometers, I wrote a few calculations into an Excel spreadsheet. I googled the values for air and helium density at different altitudes up to 39km. I found the expected burst diameters for different balloons as stated by the manufacturer. The different balloons are named based on their weights. So you can come across a Hwoyee 800g balloon, Totex 1200g balloon and so on up to 3000g, I think. The weight of the balloon is positively correlated with its burst diameter. Totex and Hwoyee are the manufacturers then.

Here is the table of balloon weights (600g-3000g) and their corresponding burst diameters (6.02m-12.00m). I chose the amount of helium and the balloon's and payload's weights as my inputs. First, I would calculate the volume of an idealized sphere of helium based on its initial weight (the weight is a constant in these calculations) at different helium densities (the values I googled corresponding to the different altitudes). From the volume, I could then calculate the sphere's diameter thus getting the balloon's expected diameter at the specific altitude.

For the values eventually used, I got the burst altitude some 300-400m short of the desired 30km. Another important number is the amount of free lift or consequently the ascent speed. In following calculations, I summed the weights of the payload (0.9kg), the balloon (0.8kg) and the helium. Out of this, I got the downward heading force acting on the balloon. If I had matched that force by the upward directed force of buoyancy, I would have made the whole balloon float. But I needed it to ascend. That is why, I had to add some amount of free lift. The overall lift force is simply the weight of the air displaced by the balloon times the acceleration of gravity (9.8). From the difference of the two forces acting on the balloon, I gained the resultant force heading upwards. Using the drag equation with this force as an input and a drag coefficient of 0.5, I could find the ascent speeds for different altitudes. Then I simply averaged them to get a single number. This value with the expected speed of descent is then used in trajectory predictors like the CUSF Landing Predictor.

To sum up the logic at play here. More helium in the balloon leads to faster ascent speed, shorter flight and thus the possibility of the balloon landing closer to you. But at the same time it means that the balloon will burst at a lower altitude. On the other hand, too little helium might result in the balloon, due to lack of the lift force, ending up floating and not reaching the burst altitude which is a problem if you want to recover the payload.

Based on these calculations, I had an idea of what sort of a balloon I needed. Now, the problem was getting it. I searched and googled and found no high altitude balloon seller in the Czech Republic and just a couple of in the US. Ordering the balloon from the US meant basically doubling the price and when I finally found a decent opportunity on Amazon, they didn't send to the Czech Republic. In the end, I managed to find a seller in the UK and order one Hwoyee 800g. The shipping cost wasn't great, but at least I finally had the balloon.

 

Once I had the balloon and the calculations done, it was time to think about how to fill it with the right amount of helium. As always, I sought inspiration in other projects. One way of accomplishing the task is to use a bottle filled with water tied to a filling hose. The filling hose is then equipped by a plastic tube at the end. The tube is used for attaching the balloon. This whole apparatus (including the water) should weigh exactly as much as the payload and the amount of free lift one desires. As the balloon fills with helium, it starts to pull on the apparatus lifting it from the ground. When it achieves this floating state one has the desired lift force.

Filling the balloon was one of the things I was a little afraid of, because it's not possible to practice it properly. The balloon is fragile, so it is advised to use latex gloves when handling it. As always, I looked for some verified method how to do this. The used tools are usually a tape, a string and some plastic strap fasteners.

First, you insert your filling tube into the balloon's thicker filling part. Then you secure it with one or two strap fasteners and the tape. The pictures are just for illustration. In reality, there would be much more tape. After that, you let the helium fill the balloon.

Once the balloon with the apparatus floats, you enclose the balloon with another pair of strap fasteners right above the end of the filling tube. You can help yourself with a string too. It's also advisable to cover the plastic straps with tape, so no sharp edges can pierce the balloon. After that, you take off the filling tube and reeve the end of the balloon through the cord to your parachute. Then you secure the folded ends of the balloon together with some more plastic straps, strings and tape. That should be it and the balloon should be securely anchored to your parachute cords.

I should explain why I in my calculations settled for an expected burst bellow the 30km altitude. It is necessary to state that the calculation is just the best guess. The current state of the atmosphere differs, or the individual balloons may be more resilient (and the experience from both mine and other projects suggests that it is often so). Aside from my own calculations, I used other estimating algorithms found on the internet to give me some feedback, and the truth is, they all differed a little bit. Some used different values for air or helium density and so on. The bottom line is that the calculations are just the best guess, but the reality will be most likely a little different.